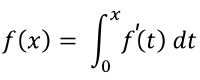瑕積分

  此條目的主題是無窮限或無界的積分。關於「廣義黎曼積分」（也簡稱「廣義積分」），請見「Henstock–Kurzweil積分」。

瑕積分（英語：Improper integral，又稱廣義積分），是對普通定積分的推廣，分成兩類。第一類瑕積分，稱為無窮積分，指積分區間的上限或下限為無窮的積分。第二類瑕積分，稱為瑕積分，指被積函數在積分區間中含有不連續點的積分。

第一類瑕積分

第一類瑕積分：上限或下限為無限的積分。

定義

第一類瑕積分是無窮積分，指積分區間的上限或下限中含有無窮 ∞ 的積分。數學定義如下：

設函數 f (x) 在 [a,+∞) 上連續且可積。定義無窮積分：

$\int_a^{\infty}f(x)\,dx=\lim_{u\to +\infty} \int_a^u f(x)\,dx$。

類似的，設函數 f (x) 在 (–∞, a] 上連續且可積。定義無窮積分：

$\int_{-\infty}^a f(x)\, dx=\lim_{u\to -\infty} \int_u^a f(x)\,dx$。

當上述極限存在時，稱該積分收斂。當上述極限不存在時，稱該積分發散。

例子如下：

$\int_1^\infty \frac{1}{x^2}\,dx=\lim_{u\to+\infty} \int_1^u\frac{1}{x^2}\,dx = 1$；

$\int_1^\infty \frac{1}{x}\,dx=\lim_{u\to+\infty} \int_1^u\frac{1}{x}\,dx = +\infty$，即發散；

$\int_1^\infty x \sin x\,dx=\lim_{u\to+\infty} \int_1^u x \sin x \,dx$ ，振動發散。

推廣定義

第一類瑕積分的定義能進一步推廣至上限及下限皆為無窮 ∞ 的積分。

設函數 f (x) 在 (–∞,+∞) 上連續且可積。定義無窮積分：

$\int_{-\infty}^\infty f(x)\,dx = \lim_{u\to -\infty} \lim_{v\to+\infty} \int_u^vf(x)\,dx$。

或者取區間上任意一點 c ，分拆寫成：

$\int_{-\infty}^\infty f(x)\,dx = \lim_{u\to -\infty} \int_u^cf(x)\,dx + \lim_{v\to+\infty} \int_c^vf(x)\,dx$。

當上述極限同時存在時，稱該積分收斂。當上述極限至少有一個不存在時，稱該積分發散。

例子如下：

$\int_{-\infty}^\infty x e^{-x^2} \,dx = \lim_{u\to -\infty} \int_u^0 x e^{-x^2}\,dx + \lim_{v\to+\infty} \int_0^v x e^{-x^2}\,dx= -\frac{1}{2} + \frac{1}{2} = 0$；

$\int_{-\infty}^\infty x \,dx = \lim_{u\to -\infty} \int_u^0 x \,dx + \lim_{v\to+\infty} \int_0^v x\,dx= -\infty + \infty$，即發散。

與柯西主值的聯繫

在無窮積分的推廣定義中，兩個極限須分別處理，即兩者的收斂速度可能不同。在柯西主值的理解下，可假設兩個極限的收斂速度相同。

設函數 f (x) 在 (–∞,+∞) 上連續且可積。定義無窮積分的柯西主值：

$\mathrm{PV}\int_{-\infty}^\infty f(x)\,dx = \lim_{R\to +\infty} \int_{-R}^Rf(x)\,dx$。

若在相同收斂速度下，兩者可以互相抵消，則該積分的柯西主值存在。舉例來說：

$\mathrm{PV}\int_{-\infty}^\infty x \,dx = \lim_{R\to +\infty} \int_{-R}^R x \,dx = 0$。

根據定義，若無窮積分收斂，則其柯西主值收斂，且二者相等。但無窮積分的柯西主值收斂，該積分未必收斂。

第二類瑕積分

第二類瑕積分：被積函數的區間中含有不連續點。

定義

第二類瑕積分是瑕積分，指積分區間的上限或下限是被積函數的不連續點。數學定義如下：

設函數 f (x) 在 (a, b] 上連續且可積，但在點 a 不連續。定義瑕積分：

$\int_a^b f(x)\,dx = \lim_{u\to a^+} \int_u^bf(x)\,dx$。

類似的，設函數 f (x) 在 [a, b) 上連續且可積，但在點 b 不連續。定義瑕積分：

$\int_a^b f(x)\,dx = \lim_{u\to b^-} \int_a^uf(x)\,dx$。

當上述極限存在時，稱該積分收斂。當上述極限不存在時，稱該積分發散。

例子如下：

$\int_0^3 \frac{1}{\sqrt{3-x}} \,dx = \lim_{u\to 3^-} \int_0^u \frac{1}{\sqrt{3-x}}\,dx=2\sqrt{3}$；

$\int_0^1 \frac{1}{x^2} \,dx = \lim_{u\to 0^+} \int_u^1 \frac{1}{x^2}\,dx=+\infty$，即發散。

推廣定義

第二類瑕積分的定義能進一步推廣至上限及下限皆為不連續點，或上限及下限之間含有不連續點的積分。

設函數 f (x) 在 (a, b) 上連續且可積，但在點 a 及 b 不連續。定義瑕積分：

$\int_a^b f(x)\,dx = \lim_{u\to a^+} \lim_{v\to b^-} \int_u^vf(x)\,dx$。

或者取區間上任意一點 c ，分拆寫成：

$\int_a^b f(x)\,dx = \lim_{u\to a^+} \int_u^cf(x)\,dx + \lim_{v\to b^-} \int_c^vf(x)\,dx$。

設函數 f (x) 在 [a, c) 及 (c, b]上連續且可積，但在點 c 不連續。定義瑕積分：

$\int_a^b f(x)\,dx = \lim_{u\to c^-} \int_a^uf(x)\,dx + \lim_{v\to c^+} \int_v^bf(x)\,dx$。

當上述極限同時存在時，稱該積分收斂。當上述極限至少有一個不存在時，稱該積分發散。

例子如下：

$\int_{-1}^{1} \frac{1}{\sqrt[3]{x^2}} \,dx = \lim_{u \to 0^-} \int_{-1}^u \frac{1}{\sqrt[3]{x^2}} \,dx + \lim_{v \to 0^+} \int_{v}^{1} \frac{1}{\sqrt[3]{x^2}} \,dx = 6$；

$\int_{-1}^{1} \frac{1}{x} \,dx = \lim_{u \to 0^-} \int_{-1}^u \frac{1}{x} \,dx + \lim_{v \to 0^+} \int_{v}^{1} \frac{1}{x} \,dx = -\infty +\infty$，即發散。

與柯西主值的聯繫

在瑕積分的推廣定義中，兩個極限須分別處理，即兩者的收斂速度可能不同。在柯西主值的理解下，可假設兩個極限的收斂速度相同。

設函數 f (x) 在 (a, b) 上連續且可積，但在點 a 及 b 不連續。定義瑕積分的柯西主值：

$\mathrm{PV}\int_a^b f(x)\,dx = \lim_{\varepsilon\to 0^+} \int_{a+\varepsilon}^{b-\varepsilon} f(x) \,dx$；

設函數 f (x) 在 [a, c) 及 (c, b]上連續且可積，但在點 c 不連續。定義瑕積分的柯西主值：

$\mathrm{PV}\int_a^b f(x)\,dx = \lim_{\varepsilon\to 0^+} \left[\int_a^{c-\varepsilon} f(x)\,dx+\int_{c+\varepsilon}^b f(x)\,dx\right]$

若在相同收斂速度下，兩者可以互相抵消，則該積分的柯西主值存在。舉例來說：

$\mathrm{PV}\int_{-1}^1 \frac{1}{x} \,dx = \lim_{\varepsilon\to 0^+} \int_{-1+\varepsilon }^{1-\varepsilon} \frac{1}{x} \,dx = 0$。

根據定義，若瑕積分收斂，則其柯西主值收斂，且二者相等。但瑕積分的柯西主值收斂，該積分未必收斂。

參考文獻

• 歐陽光中、朱學炎、陳傳璋 (2007)。《數學分析（下冊）》。第三版。高等教育出版社。ISBN 978-7-04-020743-9。
• Weisstein, Eric W. Improper Integral. From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/ImproperIntegral.html
• Weisstein, Eric W. Cauchy Principal Value. From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/CauchyPrincipalValue.html

參見

• 積分
• 極限
• 柯西主值