無理數

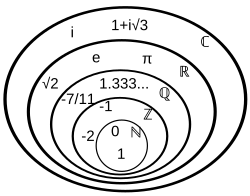
無理數是指除有理數以外的實數，當中的「理」字來自於拉丁語的rationalis，意思是「理解」，實際是拉丁文對於logos「說明」的翻譯，是指無法用兩個整數的比來說明一個無理數。

非有理數之實數，不能寫作兩整數之比。若將它寫成小數形式，小數點之後的數字有無限多個，並且不會循環，即無限不循環小數（任何有限或無限循環小數可被表示稱兩個整數的比）。常見的無理數有大部分的平方根、π和e（其中後兩者同時為超越數）等。無理數的另一特徵是無限的連分數表達式。

傳說中，無理數最早由畢達哥拉斯學派弟子希伯斯發現。他以幾何方法證明$\sqrt{2}$無法用整數及分數表示。而畢達哥拉斯深信任意數均可用整數及分數表示，不相信無理數的存在。後來希伯斯觸犯學派章程，將無理數透露給外人，因而被扔進海中處死，其罪名竟然等同於「瀆神」。另見第一次數學危機。

無理數可以通過有理數的分劃的概念進行定義。

舉例

1. $\sqrt{3}=1.73205080\cdots$
2. $\log_{10}3=0.47712125\cdots$
3. $e=2.71828182845904523536\cdots$
4. 解析失败 (转换错误。服务器（“cli”）报告：“[INVALID]”): {\displaystyle \sin{45^\circ}=\frac \sqrt 2{2}=0.70710678\cdots}
5. 圓周率=3.14159265358979323846264338327950288419716939937510582097494459230781640628620899...

性質

• 無理數加或減無理數不一定得無理數，例如:$\log_{10} 2 + \log_{10} 5 = \log_{10}10 = 1$。
• 無理數乘不等於0的有理數必得無理數。
• 無理數的平方根、立方根等次方根必得無理數。

不知是否是無理數的數

$\pi+e \,$、$\pi-e \,$等，事實上，對於任何非零整數$m \,$及$n \,$，不知道$m \pi+ne \,$是否無理數。

無理數與無理數的四則運算的結果往往不知道是否無理數，只有$\pi-\pi=0$、$\sqrt{2}+\sqrt{3}$等除外。

我們亦不知道$2^e \,$、$\pi^e \,$、$\pi^\sqrt{2}$、歐拉-馬歇羅尼常數$\gamma \,$、卡塔蘭常數$G$和費根鮑姆常數是否無理數。

無理數集的特性

無理數集是不可數集（因有理數集是可數集而實數集是不可數集）。無理數集是個不完備的拓撲空間，它是與所有正數數列的集拓撲同構的，當中的同構映射是無理數的連分數開展。因而貝爾綱定理可以應用在無數間的拓撲空間上。

無理化作連分數的表達式

$x^2=c\qquad(c>0)$，

選取一個正的實數$\rho\,$使得

$\rho^2<c\!$。

經由遞迴處理

$\begin{align} x^2\ -\!\rho^2&=c\ -\!\rho^2\\ (x\ -\!\rho)(x\ +\!\rho)&=c\ -\!\rho^2\\ x\ -\!\rho&=\frac{c\ -\!\rho^2}{\rho\ +\!x}\\ x&=\rho\ +\!\frac{c\ -\!\rho^2}{\rho\ +\!x}\\ &=\rho\ +\!\cfrac{c\ -\!\rho^2}{\rho\ +\!\left(\rho\ +\!\cfrac{c\ -\!\rho^2}{\rho\ +\!x}\right)}\\ &=\rho\ +\!\cfrac{c\ -\!\rho^2}{2\rho\ +\!\cfrac{c\ -\!\rho^2}{2\rho\ +\!\cfrac{c\ -\!\rho^2}{\ddots\,}}}=\sqrt{c}\, \end{align}$

一些無理數的證明

證明$\sqrt{2}$是無理數

證：

假設$\sqrt{2}$是有理數，並且令$\sqrt{2}=\frac{p}{q}$，$\frac{p}{q}$是最簡分數。

兩邊平方，得到$2=\frac{p^2}{q^2}$。將此式改寫為$2q^2=p^2$，可見$p^2$為偶數。

因為平方運算保持奇偶性，所以$p$只能為偶數。設$p=2p_1$，其中$p_1$為整數。

代入可得$q^2=2p_1^2$。同理可得$q$亦為偶數。

這與$\frac{p}{q}$為最簡分數的假設矛盾， 所以$\sqrt{2}$是有理數的假設不成立。

證明$\sqrt{2}+\sqrt{3}$是無理數

證：

假設$\sqrt{2}+\sqrt{3}=p$是有理數，兩邊平方得到

$5+2\sqrt{6}=p^2\Rightarrow\sqrt{6}=\frac{p^2-5}{2}$

其中因為$p$是有理數，所以$\frac{p^2-5}{2}$也是有理數。

透過證明$\sqrt{a}$為無理數的方法，其中${a}$為一非完全平方數

可以證明$\sqrt{6}$是無理數

同樣也推出$\frac{p^2-5}{2}$是無理數

但這又和$\frac{p^2-5}{2}$是有理數互相矛盾

所以$\sqrt{2}+\sqrt{3}$是一無理數

證明$\sqrt{2}+\sqrt{3}+\sqrt{5}$是無理數

證：

同樣，假設$\sqrt{2}+\sqrt{3}+\sqrt{5}=p$是有理數，兩邊平方後得到

$10+2\sqrt{6}+2\sqrt{10}+2\sqrt{15}=p^2\Rightarrow\sqrt{6}+\sqrt{10}+\sqrt{15}=\frac{p^2-10}{2}$，

於是$\sqrt{6}+\sqrt{10}+\sqrt{15}$是有理數。兩邊再次平方，得：

$31+10\sqrt{6}+6\sqrt{10}+4\sqrt{15}=\frac{(p^2-10)^2}{4}$，

於是$5\sqrt{6}+3\sqrt{10}+2\sqrt{15}=\frac{\frac{(p^2-10)^2}{8}-31}{2}$

由於$\sqrt{6}+\sqrt{10}+\sqrt{15}$是有理數，所以

$3\sqrt{6}+\sqrt{10}+2(\sqrt{6}+ \sqrt{10}+\sqrt{15})=\frac{\frac{(p^2-10)^2}{4}-31}{2}$

$\Rightarrow3\sqrt{6}+\sqrt{10}=\frac{\frac{(p^2-10)^2}{4}-31}{2}-2(\sqrt{6}+ \sqrt{10}+\sqrt{15})$

透過證明形如$\sqrt{a}+\sqrt{b}$的數是無理數的方法，得出$3\sqrt{6}+\sqrt{10}$也是一無理數

但這結果明顯和$\frac{\frac{(p^2-10)^2}{8}-31}{2}$與$2(\sqrt{6}+ \sqrt{10}+\sqrt{15})$皆為有理數出現矛盾，故$\sqrt{2}+\sqrt{3}+\sqrt{5}$為無理數

另一種證明：

同樣假設$\sqrt{2}+\sqrt{3}+\sqrt{5}=p$是有理數，

$\sqrt{2}+\sqrt{3}+\sqrt{5}=p$

$\Rightarrow\sqrt{2}+\sqrt{3}=p-\sqrt{5}$，兩邊平方：

$\Rightarrow(\sqrt{2}+\sqrt{3})^2=(p-\sqrt{5})^2$

$\Rightarrow5+2\sqrt{6}=p^2+5-2p\sqrt{5}$

$\Rightarrow2(\sqrt{6}+p\sqrt{5})=p^2$

透過證明形如$\sqrt{a}+\sqrt{b}$的數是無理數的方法，得出$\sqrt{6}+p\sqrt{5}$是一無理數

也是矛盾的。

證明$\sqrt{2}+\sqrt{3}+\sqrt{5}+\sqrt{7}$是無理數

證：

$\sqrt{2}+\sqrt{3}+\sqrt{5}+\sqrt{7}=p$

$\Rightarrow\sqrt{2}+\sqrt{3}+\sqrt{5}=p-\sqrt{7}$，兩邊平方得到：

$\Rightarrow10+2\sqrt{6}+2\sqrt{10}+2\sqrt{15}=p^2+7-2p\sqrt{7}$

$\Rightarrow\sqrt{6}+\sqrt{10}+\sqrt{15}+p\sqrt{7}=\frac{p^2}{2}-\frac{3}{2}$，得到$\sqrt{6}+\sqrt{10}+\sqrt{15}+p\sqrt{7}$為一有理數

$\Rightarrow\sqrt{6}+\sqrt{10}+\sqrt{15}=\frac{p^2}{2}-\frac{3}{2}-p\sqrt{7}$，兩邊繼續平方：

$\Rightarrow\left(\sqrt{6}+\sqrt{10}+\sqrt{15}\right)^2=\left(p^2-\frac{3}{2}-p\sqrt{7 }\right)^2$

$\Rightarrow\left(\sqrt{6}+\sqrt{10}+\sqrt{15}\right)^2=\left[\left(p^2-\frac{3}{2}\right)-p\sqrt{7 }\right]^2$

$\Rightarrow31+2\sqrt{60}+2\sqrt{90}+2\sqrt{150}=\left(p^2-\frac{3}{2}\right)^2+(-p\sqrt{7})^2-2\times{p}\sqrt{7}\times\left(p^2-\frac{3}{2}\right)$

$\Rightarrow31+4\sqrt{15}+6\sqrt{10}+10\sqrt{6}=\left(p^2-\frac{3}{2}\right)^2+7p ^2-p(2p^2-3)\sqrt{7}$

$\Rightarrow2\sqrt{10}+6\sqrt{6}+p(2p^2-3)\sqrt{7}=\left(p^2-\frac{3}{2}\right )^2+7p^2-4\left(\sqrt{6}+\sqrt{10}+\sqrt{15}+p\sqrt{7}\right)-31$

由於$\sqrt{6}+\sqrt{10}+\sqrt{15}+p\sqrt{7}$，$p$皆為有理數

設$\sqrt{10}+6\sqrt{6}+p(2p^2-3)\sqrt{7}=q=\left(p^2-\frac{3}{2}\right )^2+7p^2-4\left(\sqrt{6}+\sqrt{10}+\sqrt{15}+p\sqrt{7}\right)-31$，$q$亦為有理數

透過證明形如$\sqrt{a}+\sqrt{b}+\sqrt{c}$的數是無理數的方法，可知$\sqrt{10}+6\sqrt{6}+p(2p^2-3)\sqrt{7}$為無理數

這和$q$是有理數衝突

所以得證$\sqrt{2}+\sqrt{3}+\sqrt{5}+\sqrt{7}$為一無理數

參見

• 分劃
• 丟番圖逼近
• 3的算術平方根
• 5的算術平方根
• 超越數
• 第一次數學危機
• 正規數

外部連結

• 從畢氏學派到歐氏幾何的誕生，蔡聰明，有畢氏弄石法的證明
• $\sqrt{2}$是無理數的六個證明，香港大學數學系蕭文強（Mathematical Excalibur Vol.3 No.1 Page 2）
• 舊題新解—根號2是無理數，張海潮 張鎮華（數學傳播 第30卷 第4期）