巴斯卡三角形

《永樂大典》一頁：巴斯卡引用賈憲《釋鎖算書》中的賈憲三角形

巴斯卡三角形，又稱帕斯卡三角形、賈憲三角形、海亞姆三角形、巴斯卡三角形，是二項式系數的一種寫法，形似三角形，在中國首現於南宋杨辉的《詳解九章算法》得名，其在書中說明是引自賈憲的《釋鎖算書》，故又名賈憲三角形。前 9 行寫出來如下：

　　　　　　　　１
　　　　　　　１　１
　　　　　　１　２　１
　　　　　１　３　３　１
　　　　１　４　６　４　１
　　　１　５　10　10　５　１
　　１　６　15　20　15　６　１
　１　７　21　35　35　21　７　１
１　８　28　56　70　56　28　８　１

巴斯卡三角形第 $n$ 層（頂層稱第 0 層，第 1 行，第 $n$ 層即第 $n+1$ 行，此處 $n$ 為包含 0 在內的自然數）正好對應於二項式 $\left(a+b\right)^{n}$ 展開的係數。例如第二層 1 2 1 是冪指數為 2 的二項式 $\left(a+b\right)^{2}$ 展開形式 $a^{2}+2ab+b^{2}$ 的係數。

性質

每個數是它左上方和右上方的數的和

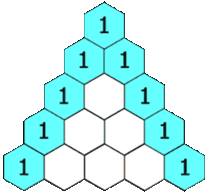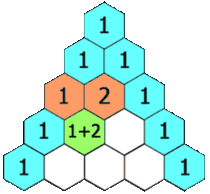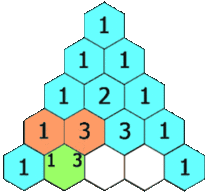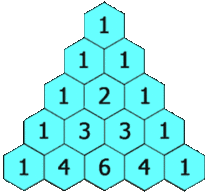
1. 巴斯卡三角形以正整數構成，數字左右對稱，每行由1開始逐漸變大，然後變小，回到1。
2. 巴斯卡三角形每一行的平方和在巴斯卡三角出現奇數次。
3. 巴斯卡三角形第2的冪行所有數都是奇數。
4. 第 $n$ 行的數字個數為 $n$ 個。
5. 第 $n$ 行的第 $k$ 個數字為組合數 $C_{k-1}^{n-1}$。
6. 第 $n$ 行數字和為 $2^{n-1}$。
7. 除每行最左側與最右側的數字以外，每個數字等於它的左上方與右上方兩個數字之和（也就是說，第 $n$ 行第 $k$ 個數字等於第 $n-1$ 行的第 $k-1$ 個數字與第 $k$ 個數字的和）。這是因為有組合恆等式：$C_{k+1}^{n+1}=C_{k}^{n}+C_{k+1}^{n}$。可用此性質寫出整個巴斯卡三角形。

歷史

朱世傑《四元玉鑒》中的「古法七乘方圖」

波斯數學家Al-Karaji和天文學家兼詩人歐瑪爾·海亞姆（عمر خیام,Omar Khayyám）在10世紀都發現了這個三角形，而且還知道可以藉助這個三角形找$n$次根，和它跟二項式的關係。但他們的著作已不存。

11世紀北宋數學家賈憲發明了賈憲三角，並發明了增乘方造表法，可以求任意高次方的展開式係數。賈憲還對賈憲三角表（古代稱數字表為「立成」）的構造進行描述。賈憲的三角表圖和文字描寫，仍保存在大英博物館所藏《永樂大典》卷一萬六千三百四十四。

13世紀中國南宋數學家巴斯卡在《詳解九章算術》裏解釋這種形式的數表，並說明此表引自11世紀前半賈憲的《釋鎖算術》。

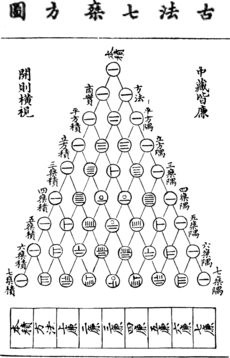
1303年元朝數學家朱世傑在《四元玉鑒》卷首繪製《古法七乘方圖》。

意大利人稱之為「塔塔利亞三角形」（Triangolo di Tartaglia）以紀念在16世紀發現一元三次方程解的塔塔利亞。

布萊士·巴斯卡的著作Traité du triangle arithmétique（1655年）介紹了這個三角形。巴斯卡搜集了幾個關於它的結果，並以此解決一些概率論上的問題，影響面廣泛，Pierre Raymond de Montmort（1708年）和亞伯拉罕·狄默夫（1730年）都用巴斯卡來稱呼這個三角形。

歷史上曾經獨立繪製過這種圖表的數學家：

• Karaji 和 Omar Khayyám 波斯 10世紀（圖文無存）
• 賈憲 中國北宋 11世紀 《釋鎖算術》 （圖文現存大英博物館所藏《永樂大典》）
• 巴斯卡 中國南宋 1261《詳解九章算法》記載之功（圖文現存大英博物館所藏《永樂大典》）
• 朱世傑 中國元朝 1299《四元玉鑒》級數求和公式
• 阿爾·卡西 阿拉伯 1427《算術的鑰匙》（現存圖文）
• 阿皮亞納斯 德國 1527
• 施蒂費爾 德國 1544《綜合算術》二項式展開式係數
• 薛貝爾 法國 1545
• B·巴斯卡 法國 1654《論算術三角形》

中國數學家的研究

中國賈憲是賈憲三角的發明人，賈憲/巴斯卡稱之為「釋鎖求廉本源」，朱世傑稱之為「古法七乘方圖」（1303年），明朝數學家吳敬《九章詳註比類算法大全》稱之為「開方作法本源」（1450年）；明王文素《算學寶鑑》稱之為「開方本源圖」（1524年）；明朝程大位《算法統宗》稱之為「開方求廉率作法本源圖」（1592年）。 清朝梅文鼎《少廣拾遺》稱之為「七乘府算法」（1692年）；清朝孔廣森《少廣正負術》稱之為「諸乘方乘率表」；焦循《加減乘除釋》稱之為「古開方本原圖」；劉衡《籌表開諸乘方捷法》稱之為「開方求廉率圖」；項名達《象數一原》稱之為「遞加圖」。偉烈亞力《數學啟蒙》稱之為「倍廉法表」；李善蘭《垛積比類》稱之為「三角垛表」。近代中算史家李儼稱之為「巴斯噶三角形」，但根據《永樂大典》指出「巴斯噶三角形」最早由賈憲使用。。著名數學家華羅庚，在1956年寫的一本通俗讀物《從巴斯卡三角談起》，將賈憲的《開方作法本源》稱為「巴斯卡三角」，首次將「巴斯噶三角形」迴歸宋朝數學家名下；此後的中學數學教科書和許多數學科普讀物都跟隨之。另一方面，專業的中國數學史著作，都用「賈憲三角」這個稱呼。。

一個數在巴斯卡三角出現的次數

由1開始，正整數在巴斯卡三角形出現的次數為：∞,1, 2, 2, 2, 3, 2, 2, 2, 4, 2, 2, 2, 2, 4, ... （OEIS:A003016）。最小而又大於1的數在賈憲三角形至少出現n次的數為2, 3, 6, 10, 120, 120, 3003, 3003, ... （OEIS:A062527）

• 除了1之外，所有正整數都出現有限次。
• 只有2出現剛好一次。
• 6,20,70等出現三次。
• 出現兩次和四次的數很多。
• 還未能找到出現剛好五次或七次的數。
• 120,210,1540等出現剛好六次。（OEIS:A098565）
  • 因為丟番圖方程
    ${n+1 \choose k+1} = {n \choose k+2},$
    有無窮個解，所以出現至少六次的數有無窮多個。
  • 其解答，是

$n = F_{2i+2} F_{2i+3} - 1,\,$
$k = F_{2i} F_{2i+3} - 1,\,$

• • 其中$F_n$表示第$n$個斐波那契數（$F_1 = F_2 = 1$）。
• 3003是第一個出現八次的數。

程式語言實現

Go

package main

import "fmt"

//行数
const LINES int = 10

//杨辉三角
func ShowYangHuiTriangle() {
	nums := []int{}
	for i := 0; i < LINES; i++ {
		//补空白
		for j := 0; j < (LINES - i); j++ {
			fmt.Print(" ")
		}

		for j := 0; j < (i + 1); j++ {
			var length = len(nums)
			var value int

			if j == 0 || j == i {
				value = 1
			} else {
				value = nums[length-i] + nums[length-i-1]
			}
			nums = append(nums, value)
			//每个数字后面加空格以间隔数字.
			fmt.Print(value, " ")
		}
		fmt.Println("")
	}
}
func main() {
	ShowYangHuiTriangle()
}

Java

public class TriangleArray
{
   public static void main(String[] args)
   {
      final int NMAX = 10; 
 
      // allocate triangular array
      int[][] odds = new int[NMAX + 1][];
      for (int n = 0; n <= NMAX; n++)
         odds[n] = new int[n + 1];  
 
      // fill triangular array
      for (int n = 0; n < odds.length; n++)
         for (int k = 0; k < odds[n].length; k++)
         {
            /*
             * compute binomial coefficient n*(n-1)*(n-2)*...*(n-k+1)/(1*2*3*...*k)
             */
            int lotteryOdds = 1;
            for (int i = 1; i <= k; i++)
               lotteryOdds = lotteryOdds * (n - i + 1) / i;
 
            odds[n][k] = lotteryOdds;
         }
 
      // print triangular array
      for (int[] row : odds)
      {
         for (int odd : row)
            System.out.printf("%4d", odd);
         System.out.println();
      }
   }
}

Python

代碼量較少的實現方式如下：

# -*- coding: utf-8 -*-
#!/usr/bin/env python
def triangles():
    L = [1]
    while True:
        yield L
        L = [sum(i) for i in zip([0]+L, L+[0])]

下面是另一種較易理解的方式：

def triangles():
    L = [1]
    S = []
    while True:
        yield L 
        L = [1] + S + [1]
        S = []
        for i in range(len(L)-1):
            S.append(L[i] + L[i+1])

Visual Basic

Private Sub Form_Click()
    N = InputBox("", "", 5)
    ReDim a(N + 1, N + 1), b(N + 1, N + 1)
    Cls
    k = 8
    For I = 1 To N
        Print String((N - I) * k / 2 + 1, " ");
        For J = 1 To I
            a(I, 1) = 1
            a(I, I) = 1
            a(I + 1, J + 1) = a(I, J) + a(I, J + 1)
            b(I, J) = Trim(Str(a(I, J)))
            Print b(I, J); String(k - Len(b(I, J)), " ");
        Next J
        Print
    Next I
End Sub

C++

//以下只有列出14行

#include<iostream>
using namespace std;
int P(int n){
	int a=1,i=1;
	while(i<=n){
		a*=i;
		i++;
	}
	return a;
}

int C(int a,int b){
	return P(a)/(P(b)*P(a-b));
}

int main(){
	for(int i=1;i<14;i++){
		for(int j=1;j<=i;j++){
			cout << C(i-1,j-1) << " ";
		}
		cout << endl;
	}
}

外部連結

• 巴斯卡三角形

參見

• 賈憲、巴斯卡
• 萊布尼茨三角形