欧拉公式

  此条目介绍的是复分析中的欧拉公式。关于代数拓扑或者多面体的欧拉公式，请见“欧拉示性数”。

  提示：此条目的主题不是欧拉定理 (几何)、欧拉定理 (数论)。

欧拉公式（英语：Euler's formula，又称尤拉公式）是复分析领域的公式，它将三角函数与复指数函数关联起来，因其提出者莱昂哈德·欧拉而得名。欧拉公式提出，对任意实数 $x$，都存在

$e^{ix} = \cos x + i\sin x$

其中 $e$ 是自然对数的底数，$i$ 是虚数单位，而 $\cos$ 和 $\sin$ 则是余弦、正弦对应的三角函数，参数 $x$ 则以弧度为单位。这一复数指数函数有时还写作 cis x （英语：cosine plus i sine，余弦加i 乘以正弦）。由于该公式在 $x$ 为复数时仍然成立，所以也有人将这一更通用的版本称为欧拉公式。

欧拉公式在数学、物理和工程领域应用广泛。物理学家理查德·费曼将欧拉公式称为：“我们的珍宝”和“数学中最非凡的公式”。

当 $x = \pi$ 时，欧拉公式变为${ {{ {e}^{{ {i}\, {\pi} }} }}+{1} } = 0$，即欧拉恒等式。

历史

约翰·伯努利注意到有

$\frac{1}{1 + x^2} = \frac12 \left( \frac{1}{1 - ix} + \frac{1}{1 + ix}\right).$

并且由于

$\int \frac{dx}{1 + ax} = \frac{1}{a} \ln(1 + ax) + C,$

上述公式通过把自然对数和复数（虚数）联系起来，告诉我们关于复对数的一些信息。然而伯努利并没有计算出这个积分。

欧拉也知道上述方程，伯努利对欧拉的回应表明他还没有完全理解复对数。欧拉指出复对数可以有无穷多个值。

与此同时，罗杰·柯特斯于 1714 年发现

$ix = \ln(\cos x + i\sin x).$

由于三角函数的周期性，一个复数可以加上 2iπ 的不同倍数，而它的复对数可以保持不变。

1740 年左右，欧拉把注意力从对数转向指数函数，得到了以他命名的欧拉公式。欧拉公式通过比较指数的级数展开和三角函数得到（其实此证法存在问题，原因见验证方法，但结论正确。），于1748 年发表。

大约 50 年之后，卡斯帕尔·韦塞尔提出可以把复数视做复平面中的点。

形式

参见：欧拉恒等式

对于任意实数$x\,$，以下等式恒成立：

$e^{ix} = \cos x+i\sin x$

由此也可以推导出

$\sin x =\frac{e^{ix}-e^{-ix}}{2i}$及$\cos x =\frac{e^{ix}+e^{-ix}}{2}$。

当$x=\pi\,$时，欧拉公式的特殊形式为

${ {{ {e}^{{ {i}\, {\pi} }} }}+{1} } = 0$。

证明

首先，在复数域上对$e^x \,$进行定义：

对于$a,b\in\mathbb{R},c=a+ib\in \mathbb{C}$，规定$e^c = \lim_{n\rightarrow\infty}(1+\frac{c}{n})^n$。

对复数的极坐标表示$w=u+iv=r(\cos\theta+i\sin\theta)$，有：

$r=\sqrt{u^2+v^2}\in\mathbb{R},\theta=\arctan(\frac{v}{u})\in\mathbb{R}$

且根据棣莫弗公式，$w^n=(u+iv)^n=r^n(\cos n\theta+i\sin n\theta)$

从而有：

$(1+\frac{a+bi}{n})^n=[(1+\frac{a}{n})+i\frac{b}{n}]^n=r_n(\cos\theta_n+i\sin\theta_n)$

假设$n>|a|$，则：

$r_n=[(1+\frac{a}{n})^2+(\frac{b}{n})^2]^\frac{n}{2},\theta_n=n\arctan\frac{\frac{b}{n}}{1+\frac{a}{n}}$

从而有：

$\begin{align} \lim_{n\rightarrow\infty}\ln r_n &=\lim_{n\rightarrow\infty}[\frac{n}{2}\ln(1+\frac{2a}{n}+\frac{a^2+b^2}{n^2})]\\ &=\lim_{n\rightarrow\infty}[\frac{n}{2}(\frac{2a}{n}+\frac{a^2+b^2}{n^2})]\\ &=a\\ \end{align}$

这一步骤用到 $\ln (1+x) \approx x$（墨卡托级数） 即：

$\lim_{n\rightarrow\infty}r_n=\lim_{n\rightarrow\infty}e^{\ln r_n}=e^a$

又有：

$\begin{align} \lim_{n\rightarrow\infty}\theta_n &=\lim_{n\rightarrow\infty}(n\arctan\frac{\frac{b}{n}}{1+\frac{a}{n}})\\ &=\lim_{n\rightarrow\infty}(n\frac{\frac{b}{n}}{1+\frac{a}{n}})\\ &=b\\ \end{align}$

从而可以证明：

$\lim_{n\rightarrow\infty}(1+\frac{a+bi}{n})^n=e^a(\cos b+i\sin b)$

即：

$e^{a+ib} = e^a(\cos b+i\sin b)$

令$a=0$，可得欧拉公式。

证毕。

验证方法

虽然下列方法（尤其是方法一）被广泛介绍，但由于在复数域中的泰勒级数展开、求导等运算均需要用到欧拉公式，造成循环论证，且有些方法在函数的定义域和性质上语焉不详，故而下列方法均应为检验方法，而非严谨的证明方法。对于类似方法也应注意甄别。

方法一：泰勒级数

把函数$e^x \,$、$\cos x\,$和$\sin x\,$写成泰勒级数形式：

$e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots$

$\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots$

$\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots$

将$x=iz\,$代入$e^x \,$可得：

$\begin{align} e^{iz} & = 1 + iz + \frac{(iz)^2}{2!} + \frac{(iz)^3}{3!} + \frac{(iz)^4}{4!} + \frac{(iz)^5}{5!} + \frac{(iz)^6}{6!} + \frac{(iz)^7}{7!} + \frac{(iz)^8}{8!} + \cdots \\ & = 1 + iz - \frac{z^2}{2!} - \frac{iz^3}{3!} + \frac{z^4}{4!} + \frac{iz^5}{5!} - \frac{z^6}{6!} - \frac{iz^7}{7!} + \frac{z^8}{8!} + \cdots \\ & = \left( 1 - \frac{z^2}{2!} + \frac{z^4}{4!} - \frac{z^6}{6!} + \frac{z^8}{8!} - \cdots \right) + i\left( z - \frac{z^3}{3!} + \frac{z^5}{5!} - \frac{z^7}{7!} + \cdots \right) \\ & = \cos z + i\sin z \end{align}$

方法二：求导法

对于所有$x \in I$，定义函数$f(x)=\frac{\cos x+i\sin x}{e^{ix}}$

由于$e^{ix}\cdot e^{-ix}=e^0=1$

可知$e^{ix}\,$不可能为0，因此以上定义成立。

$f(x)\,$之导数为：

$\begin{align} f'(x)& = \frac{(-\sin x+i\cos x)\cdot e^{ix} - (\cos x+i\sin x)\cdot i\cdot e^{ix}}{(e^{ix})^2} \\ & = \frac{-\sin x\cdot e^{ix}-i^2\sin x\cdot e^{ix}}{(e^{ix})^2} \\ & = \frac{-\sin x\cdot e^{ix}+\sin x\cdot e^{ix}}{(e^{ix})^2} \\ & = 0 \end{align}$

设$[a,b] \in I$和$c \in (a,b)$

$f'(c)=\frac{f(b)-f(a)}{b-a}.$（拉格朗日中值定理）

$\because f'(x)=0$

$\therefore f'(c)=0$

$f(a)=f(b)$

因此$f(x)\,$必是常数函数。

$f(x)=f(0)$

$\frac{\cos x + i \sin x}{e^{ix}} =\frac{\cos 0 + i \sin 0}{e^0} =1$

重新整理，即可得到：

$e^{ix} = \cos x + i\sin x$

方法三：微积分

找出一个函数，使得$\frac{dy}{dx}=iy$及$f(0)=1$

$\frac{d}{dx}e^{ix}=ie^{ix}=iy$

$\begin{align}\frac{d}{dx}(\cos x+i \sin x) &= -\sin x + i \cos x \\ & =i (i \sin x + \cos x) \\ &=iy\end{align}$

$e^{i0}=e^{0}=1$

$\cos0 +i\sin 0=1+i(0)=1$

如果使用积分法，$iy$的原函数是以上两个函数。

$x=0$时，原函数的值相等，所以以上两个函数相等。

$e^{ix} = \cos x + i\sin x$

cis函数

主条目：Cis函数

在复分析领域，欧拉公式亦可以以函数的形式表示

$\operatorname{cis} \theta = \cos \theta+i\sin \theta$

$\operatorname{cis} \theta = e^{i\theta}$

并且一般定义域为$\theta \in \mathbb{R}\,$，值域为$\theta \in \mathbb{C}\,$（复平面上的所有单位向量）。

当一复数的模为1，其反函数就是辐角（arg函数）。

当$\theta$值为复数时，cis函数仍然是有效的，所以有些人可利用cis函数将欧拉公式推广到更复杂的版本。

证明和角公式

由于$e^{i \alpha}=\cos \alpha+i \sin \alpha$且$e^{i \beta}=\cos \beta+i \sin \beta$，则有

$\begin{align} e^{i (\alpha+\beta)}&=\cos (\alpha+ \beta)+i\sin (\alpha+ \beta) =e^{i \alpha+i \beta}\\ &=e^{i \alpha} \times e^{i \beta}\\ & =(\cos \alpha + i\sin \alpha) \times (\cos \beta + i\sin \beta)\\ & =(\cos \alpha \times \cos \beta+i\sin \alpha \times i\sin \beta)+(i\sin \alpha \times \cos \beta+\cos \alpha \times i\sin \beta)\\ & =(\cos \alpha \cos \beta-\sin \alpha \sin \beta)+i(\sin \alpha \cos \beta+\cos \alpha \sin \beta)\\ \end{align}$

实部等于实部，虚部等于虚部，因此

$\cos (\alpha+ \beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta$

$\sin (\alpha+ \beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta$

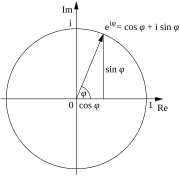
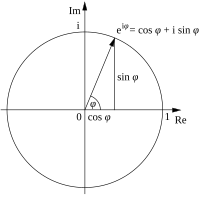
在复分析的应用

这公式可以说明当 $x$ 为实数时，函数 $e^{ix}$ 可在复数平面描述一单位圆。且 $x$ 为此平面上一条连至原点的线与正实轴的交角。先前一个在复平面的复点只能用笛卡尔坐标系描述，欧拉公式在此提供复点至极坐标的变换

任何复数 $z=x+yi$ 皆可记为

$z = x + iy = |z| (\cos \phi + i\sin \phi ) = |z| e^{i \phi} \,$

$\bar{z} = x - iy = |z| (\cos \phi - i\sin \phi ) = |z| e^{-i \phi} \,$

在此

$x = \mathrm{Re}\{z\} \,$为实部

$y = \mathrm{Im}\{z\} \,$为虚部

$|z| = \sqrt{x^2+y^2}$为 $z$ 的模

$\phi = \mathrm{atan2}{(y,x)}$，其中 $\mathrm{atan2}{(y,x)}= \begin{cases} \arctan\left(\frac y x\right) & \qquad x > 0 \\ \pi + \arctan\left(\frac y x\right) & \qquad y \ge 0 , x < 0 \\ -\pi + \arctan\left(\frac y x\right) & \qquad y < 0 , x < 0 \\ \frac{\pi}{2} & \qquad y > 0 , x = 0 \\ -\frac{\pi}{2} & \qquad y < 0 , x = 0 \\ \text{undefined} & \qquad y = 0, x = 0 \end{cases}$

参见

• cis函数
• 欧拉恒等式